Арифметикалык сериядагы терминдердин санын табуу оор сезилиши мүмкүн, бирок чындыгында бул абдан жөнөкөй. Сиз жөн гана U формуласына сандарды киргизишиңиз керек = a + (n - 1) b жана терминдердин саны болгон n маанисин табыңыз. Билгиле, У сериядагы акыркы сан, а - сериядагы биринчи термин, b - чектеш шарттардын ортосундагы айырма.
Кадам
Кадам 1. Сериянын биринчи, экинчи жана акыркы терминдерин аныктаңыз
Адатта, ушул сыяктуу суроолор биринчи 3 же андан көп терминди жана акыркы терминди берет.
Мисалы, сиздин сурооңуз мындай: 107, 101, 95… -61. Бул учурда, биринчи чейреги 107 жана акыркы мөөнөтү -61. Маселени чечүү үчүн сизге бул маалыматтын баары керек
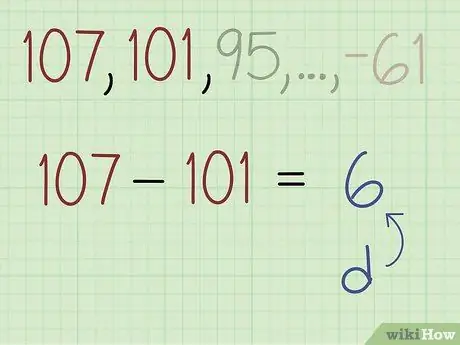
2 -кадам. (B) айырмасын табуу үчүн биринчи мүчөдөн экинчи мүчөнү алып салыңыз
Мисал маселесинде биринчи термин 107, экинчи термин 101. Айырманы табуу үчүн 101ди 107ге азайтып, -6 алыңыз.
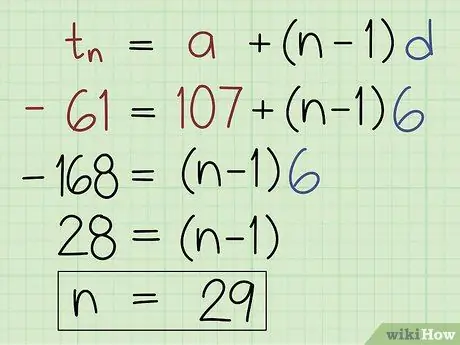
3 -кадам. U формуласын колдонуңуз = a + (n - 1) b n табуу үчүн.
Акыркы мөөнөттү киргизиңиз (U ), биринчи термин (а) жана айырма (б). N маанисин алганга чейин теңдемелерди санап чыгыңыз.
