Сиз калькуляторду колдонбой сызыктуу теңдемелерди кантип чийүүнү билбейсизби? Бактыга жараша, эгер сиз билсеңиз, сызыктуу теңдемелерди чийүү абдан оңой. Болгону теңдемеңиз жөнүндө бир нече нерсени түшүнүшүңүз керек жана сиз муну кыла аласыз. Баштайлы.
Кадам
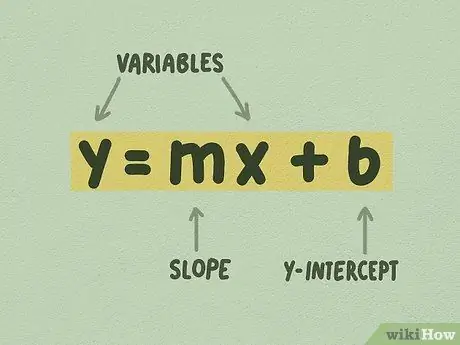
Кадам 1. Сызыктуу теңдеме y = mx + b түрүнө ээ экенин текшериңиз
Бул форма y-intercept формасы деп аталат жана, балким, сызыктуу теңдемелерди графикалоодо колдонуунун эң оңой формасы. Теңдемедеги маани бүтүн сан болушу шарт эмес. Көбүнчө сиз мындай окшоштукту көрөсүз: y = 1/4x + 5, мында 1/4 m жана 5 b.
- м "жантаюу", же кээде "градиент" деп аталат. Капталдын жогорулашы же y өзгөрүүсү x өзгөрүүсүнө бөлүнүү катары аныкталат.
- b "y-intercept" деп аныкталат. У-кесилиш сызык Y огу менен кесилишкен чекит.
- x жана y - өзгөрмөлөр. Сиз белгилүү бир х маанисин чече аласыз, мисалы, эгер сизде y чекити болсо жана m жана b маанилерин билсеңиз. Бирок, х, эч качан бир гана мааниге ээ эмес: анын мааниси сызык өйдө же ылдый карай өзгөрөт.
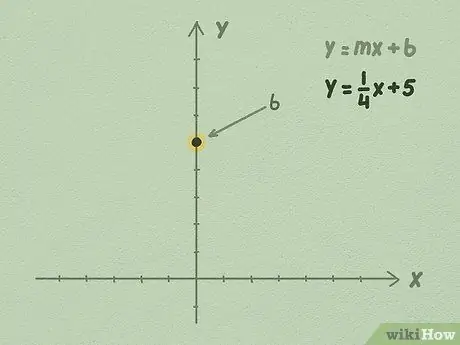
2 -кадам. Y огунда b санын тартыңыз
Сиздин b мааниси ар дайым рационалдуу сан болуп калат. B саны кандай болбосун, Y огунда анын маанисин табыңыз жана вертикалдуу огунун чекитине коюңуз.
Мисалы, y = 1/4x + 5 барабардыгын колдонолу. Акыркы сан б болгондуктан, б 5ке барабар экенин билебиз. Y огунда 5 чекитти жогору жылдырып, чекиттерди белгилеңиз. Бул жерде сиздин түз сызыгыңыз Y огу менен кесилишет
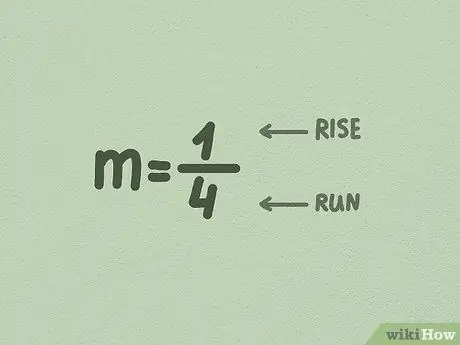
3 -кадам. Mны бөлчөккө айландыруу
Көбүнчө, xтин алдындагы сан мурунтан эле бир бөлүк, андыктан аны алмаштыруунун кажети жок. Бирок андай болбосо, жөн гана 1дин астына m маанисин коюп, аны өзгөртүңүз.
- Биринчи сан (эсептегич) - бул өсүштүн капталга бөлүнүшү. Бул сан сызыктын канчалык өйдө же тигинен кеткенин көрсөтөт.
- Экинчи сан (бөлгүч) - жогорулап бараткан каптал. Бул сан сызыктын канчалык жанаша же горизонталдуу жылганын көрсөтөт.
- Мисалы:
- 4/1 жантайышы капталга ар бир 1 пункт үчүн 4 пунктка жогору жылат.
- -2/1 жантайышы капталга ар бир 1 чекит үчүн 2 пунктка ылдый жылат.
- 1/5 жантайышы капталга карай ар бир 5 чекит үчүн 1 пунктка өйдө жылат.
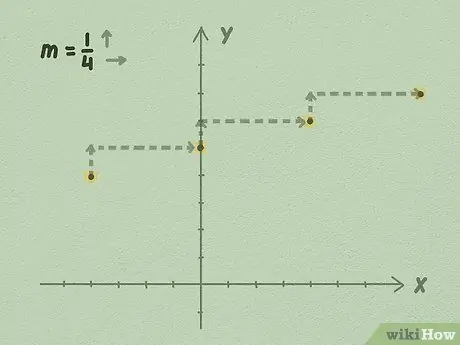
Кадам 4. жантыкты колдонуу менен линияны bден узартууну баштаңыз, же өйдө тарапка бөлүңүз
B маанисиңизден баштаңыз: биз теңдеме ушул чекиттен өткөнүн билебиз. Теңдемедеги упайларды алуу үчүн эңкейишти алуу жана анын маанисин колдонуу менен линияны кеңейтиңиз.
- Мисалы, жогорудагы сүрөттү колдонуп, ар бир 1 пунктка жогору, сызык 4 чекитти оңго жылдырганын көрө аласыз. Бул сызыктын эңкейиши 1/4 болгон үчүн болот. Сиз сызыкты график үчүн тарапка бөлүнгөн колдонууну улантып, эки тарапка тең белгисиз мөөнөткө узартасыз.
- Жантайыңкы өйдө жылганда оң, ал эми ылдый түшүүдө терс болот. Мисалы, -1/4 жантайышы ар бир 4 пунктка капталга 1 пунктка ылдый жылат.
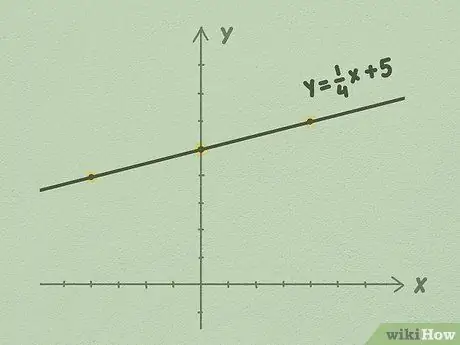
Кадам 5. Сызыкты кеңейтүүнү улантыңыз, сызгычты колдонуңуз жана эңкейишти, м, колдонуучу катары колдонууну тактаңыз
Сызыкты белгисиз мөөнөткө узартыңыз жана сызыктуу теңдемеңиздин графигин түзүп бүттүңүз. Абдан оңой, туурабы?
