Калькуляторсуз квадрат тамырын табуунун 3 жолу

2024 Автор: Jason Gerald | [email protected]. Акыркы өзгөртүү: 2023-12-16 11:24

Сандын квадрат тамырын, эгерде жооп бүтүн сан болсо, оңой эле табууга болот. Эгерде жооп бүтүн сан болбосо, сиз калькуляторду колдонбосоңуз да, квадрат тамырды алуу үчүн бир нече процесстерди аткарсаңыз болот. Бул үчүн сиз көбөйтүүнүн, кошуунун жана бөлүүнүн негиздерин түшүнүшүңүз керек.

Кадам

3 методу 1: Бүтүн сандын квадрат тамырын табуу

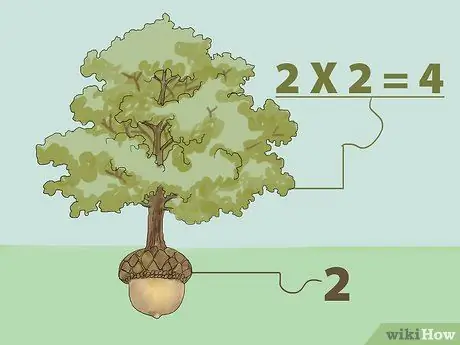
Кадам 1. Көбөйтүү аркылуу кемчиликсиз квадрат тамырды табыңыз

Сандын квадрат тамыры - бул өзү көбөйтүлгөндө баштапкы санды кайтарган сан. Башкача айтканда: "Биз каалаган санды алуу үчүн кайсы санды өзүбүз көбөйтө алабыз?"

Мисалы, 1дин квадрат тамыры 1, анткени 1дин 1ге көбөйтүлүшү 1 (1X1 = 1). Ошентип, 4 квадрат тамыры 2, анткени 2 2ге көбөйтүлгөндө 4 болот (2X2 = 4). Квадрат тамыр түшүнүгүн дарак деп ойлогула. Дарак уруктан өсөт. Демек, дарак үрөндөн чоңураак, анын тамыры болгон уруктан өсөт. Жогорудагы мисалдан 4 - дарак, 2 - үрөн.
Ошентип, 9дун квадрат тамыры 3 (3X3 = 9), 16нын 4ү (4X4 = 16), 25тин 5и (5X5 = 25), 36сынын 6сы (6X6 = 36), 49унун 7си (7X7 = 49), 64төн 8ге (8X8 = 64), 81ден 9га (9X9 = 81), 100дөн 10го (10X10 = 100).

Калькулятору жок төрт бурчтуу тамыр табыңыз 2 -кадам

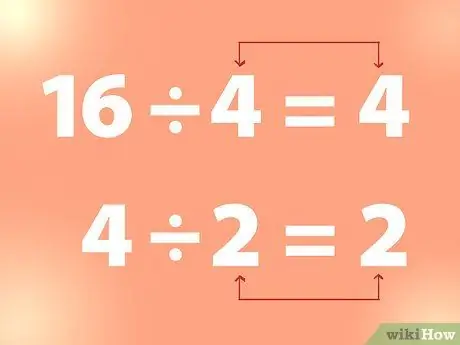
Кадам 2. Квадрат тамырды табуу үчүн үзгүлтүксүз бөлүнүүнү колдонуңуз

Бүтүн сандын квадрат тамырын табуу үчүн, бөлгүчкө барабар болгон сан келгенге чейин бүтүн санды санга бөлүүгө болот.

Мисал: 4тү 4кө бөлүү 4. Ал эми 4тү 2ге бөлүү 2, ж.б. Ошентип, жогорудагы мисалдан, 4 - 16нын квадрат тамыры жана 2 - 4түн квадрат тамыры.
Perfect квадрат тамырларда эч кандай бөлчөк же ондук болбойт, анткени алар бүтүн сандар.

Калькулятору жок төрт бурчтуу тамыр табыңыз 3 -кадам

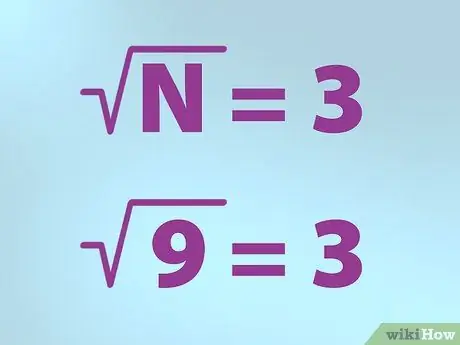
Кадам 3. Квадрат тамыр үчүн туура белгини колдонуңуз

Математиктер квадрат тамырды көрсөтүү үчүн атайын белгини колдонушат. Формасы текшерүү белгисине окшош, оң жактагы жогорку сызыгы бар.

N квадрат тамырды тапкыңыз келген санга барабар. N белгинин астына коюлган.
Демек, эгерде сиз 9дун квадрат тамырын тапкыңыз келсе, анда "N" (9) белгисине коюп ("тамыры" тамгасы) менен формуланы жазыңыз, андан кийин барабар белгини жазыңыз жана анын артынан 3 белгисин жазыңыз. 9 3 "барабар.

Метод 2 3: Башка сандын квадрат тамырын табуу

Калькулятору жок төрт бурчтуу тамыр табыңыз 4 -кадам

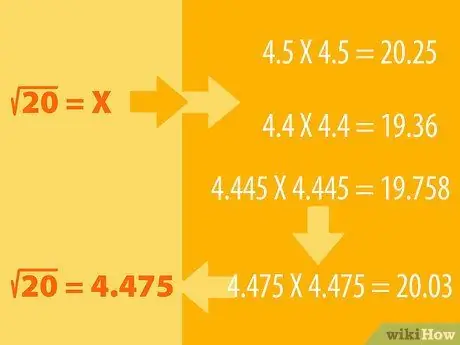
Кадам 1. Ойлоп көрүңүз жана жок кылуу процессин аткарыңыз

Бүтүн эмес сандын квадрат тамырын табуу кыйын. Бирок, бул мүмкүн эмес дегенди билдирбейт.

Мисалы, 20нын квадрат тамырын тапкыңыз келет дейли. Биз билебиз, 16 - бул кемчиликсиз бир квадрат, анын квадрат тамыры 4 (4X4 = 16). Андан кийин 25 чарчы тамыры 5 (5X5 = 25), ошондуктан 20нын квадрат тамыры экөөнүн ортосунда жатышы керек.
Сиз 20 санынын квадрат тамыры 4,5 деп болжой аласыз. Эми жыйынтыкты көрүү үчүн 4.5 чарчы. Башкача айтканда, биз 4, 5ти өзүбүзгө көбөйтөбүз: 4, 5X4, 5. Жооп 20дан көп же аз экенин караңыз, эгер сиздин божомолуңуз өтө алыс болсо, башка номерди колдонуп көрүңүз (мис. 4, 6 же 4, 4) жана тууралаңыз болжол боюнча. сиз 20 санын алганга чейин.
Мисалы, 4, 5X4, 5 = 20, 25, логикалык жактан биз кичине санды табышыбыз керек, балким 4, 4. 4, 4X4, 4 = 19, 36. Демек, 20 санынын квадрат тамыры 4, 5 жана 4, 4. 4, 445X4, 445 менен аракет кылыңыз. Жыйынтык 19, 758. Жыйынтык жакындап келе жатат. 4, 475X4, 475 = 20, 03 алганга чейин башка сандар менен аракет кыла бериңиз. Тегеректелгенде, бул сан 20га барабар.

Калькулятору жок төрт бурчтуу тамыр табыңыз 5 -кадам

Кадам 2. Орточо жараянды колдонуңуз

Бул процесс ошондой эле сан менен капталган эң жакын эки кемчиликсиз квадратты табуудан башталат.

Андан кийин бул санды кемчиликсиз квадрат тамырлардын бирине бөлүңүз. Жоопту алыңыз, андан кийин ошол сан менен тамырын тапкыңыз келген сан ортосундагы орточо табыңыз (экөөнү кошуп, экиге бөлүү менен орточо көрсөткүчтү таба аласыз). Андан кийин алынган санды баштапкы санга бөлүңүз. Акыркы кадам, биринчи жолу эсептелген орточо жыйынтыктардын орточо санын табуу.
Үн татаалбы? Мисал келтирсе оңой болмок. Мисалы, 10 9 (3X3 = 9) жана 16 (4X4 = 16) эки кемчиликсиз квадраттардын ортосунда жатат. Экөөнүн тең квадрат тамырлары 3 жана 4. Ошентип, 10ду биринчи санга бөлгүлө, 3. Жыйынтык 3, 33. Эми 3 жана 3, 33түн ортолорун кошуп, 2ге бөлүү менен табыңыз. 3, 1667 Азыр 10ду 3.1667ге бөлгүлө. Жыйынтыгы 3.1579. Андан кийин 3.1579 менен 3.1667дин орточо санын кошуп, 2ге бөлүү менен табыңыз. Жыйынтык 3.1623.
Жоопту өзүңүз текшериңиз (бул мисалда 3, 1623). 3.1623 жыйынтыгы 3.1623кө көбөйтүлгөндө 10.001 болуп чыгат.

3 -метод 3: Терс сандарды квадраттоо

Калькулятору жок төрт бурчтуу тамыр табыңыз 6 -кадам

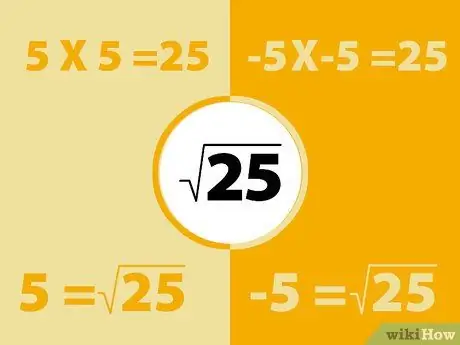
1 -кадам. Ошол эле ыкманы колдонуу менен терс сандарды квадраттаңыз

Негатив жолу терс оң экенин унутпаңыз. Ошентип, терс сандын квадраты оң санды чыгарат.

Мисалы, -5X -5 = 25. Бирок, 5x5 = 25 экенин да унутпаңыз. Ошентип, 25тин квадрат тамыры -5 же 5. болушу мүмкүн. Негизинен ар бир сандын эки чарчы тамыры бар.
Ошо сыяктуу эле, 3X3 = 9 жана -3X -3 = 9, ошондуктан 9дун квадрат тамырлары 3 жана -3. Оң квадрат тамыр "негизги тамыр" деп аталат. Бул жерде биз жөн гана бул жоопко көңүл буруубуз керек.

Калькулятору жок төрт бурчтуу тамыр табыңыз 7 -кадам

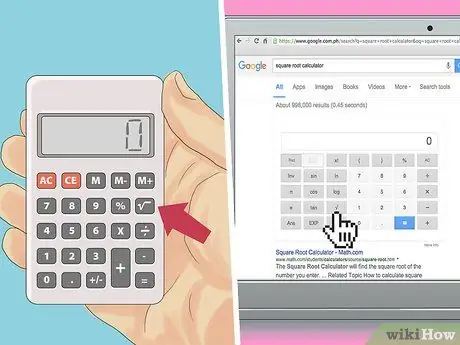
Кадам 2. Калькуляторду колдонуңуз

Математиканы кол менен жасоо эң жакшы болгону менен, квадрат тамырларды эсептөө үчүн көптөгөн онлайн эсептегичтер бар.

Кадимки эсептегичтен квадрат тамырдын баскычын издеңиз.
Онлайн калькулятордо, квадрат тамырдын маанисин тапкыңыз келген санды түздөн -түз киргизип, баскычты басыңыз. Компьютер сизге квадрат тамырын көрсөтөт.

Кеңештер

Ар дайым бир нече маанилүү кемчиликсиз квадраттарды эске алыңыз:
- 0² = 0, 1² = 1, 3² = 9, 4² = 16, 5² = 25, 6² = 36, 7² = 49, 8² = 64, 9² = 81, 10² = 100,
- Бул кемчиликсиз квадратты эстен чыгарбаңыз: 11² = 121, 12² = 144, 13² 169, 14² = 196, 15² = 225, 16² = 256, 17² = 289…
- Муну да эске алыңыз: 10² = 100, 20² = 400, 30² = 900, 40² = 1600, 50² = 2500, …